欧拉回路和欧拉路径

欧拉回路与欧拉路径是图论中的经典概念之一。若图中的一条路径从某个节点出发，经过每条边恰好一次，并回到起点，则称该路径为欧拉回路。若只要求路径经过每条边恰好一次，不要求其回到起点，则称该路径为欧拉路径。

一张无向图中存在欧拉回路，当且仅当所有非零度节点（有边连接的节点）是连通的，且每个节点的度数均为偶数。（有进入节点的边就需要有出节点的边，度数是2的倍数）

无向图的Hierholzer 算法

上述分析只能说明，当图中存在度数为奇数的节点时，不存在欧拉回路。我们还需要一个用来找出欧拉回路的算法，才能证明当所有节点度数为偶数时，欧拉回路确实存在。

Hierholzer 的基本思想是首先找到一个子回路，并逐步将其他回路合并到该子回路中，最终形成完整的欧拉回路。该证明被后人整理成 Hierholzer 算法，用于在已经判定无向图的欧拉回路存在的前提下，找出一条欧拉回路。算法流程如下：

1. （寻找子回路）从任意非零度节点 出发，沿着边遍历图。在遍历过程中，删除经过的边。如果遇到一个所有边都被删除的节点，那么该节点必然是 （证明见下文），即我们找到了一个包含 的回路。将该回路上的节点和边添加到结果序列中。
2. （检查是否存在其它回路）检查刚刚添加到结果序列中的节点，看是否还有与节点相连，且未遍历的边。如果发现节点 有未遍历的边，则从 出发重复步骤 1，找到一个包含 的新回路，将结果序列中的一个 用这个新回路替换。此时结果序列仍然是一个回路，只不过变得更长了。
3. （结束条件）重复步骤 2，直到所有边都被遍历。此时结果序列中的节点和边就构成了欧拉回路。算法结束。

算法流程演示

算法流程可能有一些复杂，我们通过一个例子来理解算法的执行步骤。例如，考虑用 Hierholzer 算法找出下图的欧拉回路。

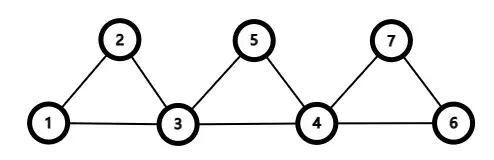
首先进行步骤 1 。从任意节点出发（不妨从节点1 出发），沿着边遍历图，删除经过的边，直到无法继续前进。假设我们的遍历路径为1-2-3-1 ，此时我们找到了一个包含1 的回路。将该回路添加到结果序列中，此时的结果序列即为1-2-3-1 ，而图也变成了下面的样子。

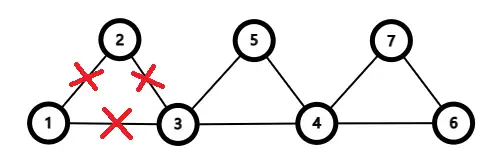
接下来进行步骤 2 。检查刚刚添加到结果序列中的节点（节点 1、2 、3 ）。我们发现，节点 还存在未被遍历的边（ 3-4和3-5 ），因此我们从节点3出发，重复步骤 1。假设我们的遍历路径为3-4-5-3，此时我们找到了一个包含3的回路。将结果序列中的一个3换成这个回路，此时的结果序列即为1-2-(3-4-5-3)-1 ，而图也变成了下面的样子。

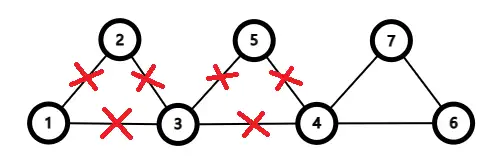
重复进行步骤 2 。检查刚刚添加到结果序列中的节点（节点 3、4、5）。我们发现，节点 还存在未被遍历的边（ 4-7和4-6 ），因此我们从节点 4出发，重复步骤 1。假设我们的遍历路径为4-7-6-4 ，此时我们找到了一个包含4的回路。将结果序列中的一个4换成这个回路，此时的结果序列即为 1-2-3-(4-6-7-4)-5-3-1，而图也变成了下面的样子。

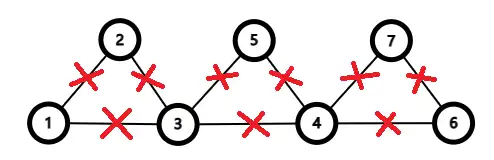
重复进行步骤 2。检查刚刚添加到结果序列中的节点（节点 4、6、7）。此时不存在未遍历的边，因此结果序列 1-2-3-4-6-7-4-5-3-1就是原图中的一个欧拉回路。算法结束。

算法代码实现

这里用到了链式前向星存图( oi-wiki的介绍和csdn上讲解比较清楚的文章)

在图论的代码实现中，一条无向边一般会被拆成两条有向边。由于 Hierholzer 算法的流程需要我们删除一条无向边，因此我们需要同时删除一条有向边和它的反向边。这样的操作只有利用链式前向星[^6](https://link.zhihu.com/?target=https%3A//oi-wiki.org/graph/save/%23%E9%93%BE%E5%BC%8F%E5%89%8D%E5%90%91%E6%98%9F)（亦称边表）存储无向图时才能在O(1)的时间复杂度内完成，因此下文的代码实现中，均使用链式前向星存储无向图。

Hierholzer 算法的一个 C++ 实现如下。请注意，为了便于分析与讲解，下面给出的代码实现并不是欧拉回路的最优时间复杂度实现。

// 为了方便存储一条边的众多信息，我们定义一个结构体
//
// struct Edge {
//     int fn, nxt;
//     bool del;
// };
//
// 其中：
//   * fn 表示这条有向边的终点
//   * nxt 表示链式前向星中，该有向边的后续边的编号，如果没有后续边则值为 0
//   * del 表示这条边是否被遍历过了
//
// e[] 是一个类型为 Edge 的数组，e[i] 表示链式前向星中编号为 i 的边
// p[] 是一个类型为 int 的数组，p[i] 表示以 i 为起点的第一条边在链式前向星中的编号
// 如果没有以 i 为起点的有向边则 p[i] 的值为 0
//
// 为了方便我们查找某一条有向边的反向边，当我们向链式前向星中加入第 i（i 从 1 到 m）条无向边 x - y 时，
// 我们会将有向边 x -> y 存储在 e[i * 2]，有向边 y -> x 存储在 e[i * 2 + 1]，
// 这样，e[i] 和 e[i ^ 1] 就互为反向边
//
// ans 是一个类型为 vector<Edge> 的变量，用来存储我们找到的回路

void dfs(int sn) {
    for (int i = p[sn]; i != 0; i = e[i].nxt) {
        // 这条边已经被遍历过了，跳过
        if (e[i].del) continue;
        // 删除有向边 e[i] 和它的反向边 e[i ^ 1]
        e[i].del = e[i ^ 1].del = true;
        // 继续遍历相邻点
        dfs(e[i].fn);
        // 将边 e[i] 加入结果序列中
        ans.push_back(e[i]);
    }
}

调用 dfs(S) 后，ans 里就保存了从节点 S 出发，并回到节点 S 的欧拉回路。需要注意的是，此时 ans 中保存的欧拉回路，是我们求出的欧拉回路的倒序。因此，我们还需要调用 reverse(ans.begin(), ans.end()) 将 ans 中所有元素顺序倒转后，才能得到我们想要的欧拉回路。

代码执行演示

读者可能很难相信，如此简单的代码就能完成从找环到判别到插入环的所有步骤。读者可能还会非常疑惑，为什么需要在 dfs 回溯的时候，才将边加入结果序列中？为什么 ans 中存储的是欧拉回路的倒序？让我们通过一个例子来理解这段代码实现的精妙之处。

考虑下面这张仅由一个环组成的图。

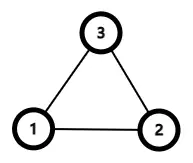
当我们调用 dfs(1) 时，上述实现会以 dfs(1) -> dfs(2) -> dfs(3) -> dfs(1) 的顺序逐层递归。由于节点 此时不存在未被遍历的边，我们找到了一个包含节点 的回路，dfs 也将开始回溯。这正是 Hierholzer 算法流程中的步骤 1（寻找子回路）。

其它节点此时也都不存在未被遍历的边，因此每一层 dfs 的 for 循环都不会被再次运行，而是继续回溯。这正是 Hierholzer 算法流程中的步骤 2（检查是否存在其它回路），只是我们没有找到其它回路。

由于 e[i] 在 dfs 回溯的过程中才被加入 ans，因此回溯结束后，ans 中保存的边为 [3 -> 1, 2 -> 3, 1 -> 2]，正是包含节点 的回路的倒序。

让我们在图中增加两个节点，看看递归过程会发生什么变化。

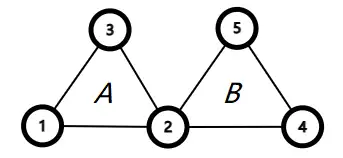
当我们调用 dfs(1) 时，假设上述实现仍然以 dfs(1) -> dfs(2) -> dfs(3) -> dfs(1) 的顺序逐层递归。由于节点 此时不存在未被遍历的边，我们找到了一个包含节点 的回路 ，dfs 也将开始回溯。这一步和前一张图没有什么差别。

当回溯到 dfs(2) 时，此时 ans 中保存的边为 [3 -> 1, 2 -> 3]。由于节点 存在未被遍历的边（ 与 ），因此对回路 的记录将暂停。dfs(2) 重新进入 for 循环，开始寻找包含节点 ，且第一条边是 的回路。这正是 Hierholzer 算法流程中的步骤 2（检查是否存在其它回路），而且我们发现存在包含节点 的回路。

开始寻找包含节点 的回路后，上述实现将以 [dfs(1) -> dfs(2)] -> dfs(4) -> dfs(5) -> dfs(2) 的顺序逐层递归。由于节点 此时不存在未被遍历的边，我们找到了一个包含节点 的回路 ，dfs 也将开始回溯。这就重新执行了 Hierholzer 算法流程中的步骤 1（寻找子回路）。

其它节点此时也都不存在未被遍历的边，因此每一层 dfs 的 for 循环都不会被再次运行，而是继续回溯。当重新回溯到 dfs(2) 时，此时 ans 中保存的边为 [3 -> 1, 2 -> 3, 5 -> 2, 4 -> 5, 2 -> 4]。可以看到，我们将回路 的倒序插在了（未完成的）回路 的倒序里。回路 的回溯重新开始。

回溯结束后，ans 中保存的边为 [3 -> 1, 2 -> 3, 5 -> 2, 4 -> 5, 2 -> 4, 1 -> 2]。这正是我们要求的欧拉回路的倒序。

哈密顿路径和哈姆顿环、哈密顿图、半哈密顿图

通过图中所有顶点一次且仅一次的通路称为哈密顿通路。

通过图中所有顶点一次且仅一次的回路称为哈密顿回路。

具有哈密顿回路的图称为哈密顿图。

具有哈密顿通路而不具有哈密顿回路的图称为半哈密顿图。

狄拉克定理

n个顶点的简单图（n>=3）中，若每个顶点的度皆至少为n/2，则必为哈密顿图。

欧尔定理

设G=(V,E)是一个无向简单图，

V

=n ,n > 3。 若对于任意两个不相邻的顶点u,v 属于 V，都有d(n)+

d(v) >= n , 那么G是哈密顿图

图论中的经典问题哈密顿路径问题与哈密顿环问题分别是来确定在一个给定的图上是否存在哈密顿路径（一条经过图上每个顶点的路径）和哈密顿环（一条经过图上每个顶点的环）。两个问题皆为NP完全。