数学建模之规划模型

kevin 2023-04-22

数学规划模型

线性规划，非线性规划，整数规划，最大最小化以及多目标规划的Matlab使用（不涉及数学原理）

  • 线性规划：目标函数和和约束条件均是决策变量的线性表达式
[x fval] = linprog(c, A, b, Aeq, beq, lb,ub, x0)
% c是目标函数的系数向量，A是不等式约束Ax<=b的系数矩阵，b是不等式约束Ax<=b的常数项
% Aeq是等式约束Aeq x=beq的系数矩阵，beq是等式约束Aeq x=beq的常数项
% lb是X的下限，ub是X的上限，X是向量[x1,x2,...xn]' , 即决策变量。
% 迭代的初始值为x0（一般不用给）
% 不存在不等式约束, 可用"[]"替代A和b
% 不存在等式约束, 可用"[]"替代Aeq和beg
% 返回的x是取最小值时的取值，fval是最小值
% 若要求的是max z，可转换为min -z, 然后答案取-fval
  • 非线性规划：目标函数和或者约束条件中有一个是决策变量x的非线性表达式，没有通用算法, 大多数算法都是在选定决策变量的初始值后, 通过搜索方法 （蒙特卡罗模拟）
[x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)
% x0表示给定的初始值（用行向量或者列向量表示），必须得写
% A b表示线性不等式约束
% Aeq beq 表示线性等式约束
% lb ub 表示上下界约束
% @fun表示目标函数
% @nonlfun表示非线性约束的函数
% option 表示求解非线性规划使用的方法
  • 整数规划是一类要求变量取整数值的数学规划，目前流行的求解整数规划的算法往往只适用于线性整数规划，特例：0-1规划
[x,fval] =  intlinprog(c,intcon, A, b, Aeq, beq, lb,ub)
% 例如决策变量有三个: x1, x2, x3,若x1和x3是整数 则intcon=[1,3]

  • 最大最小化

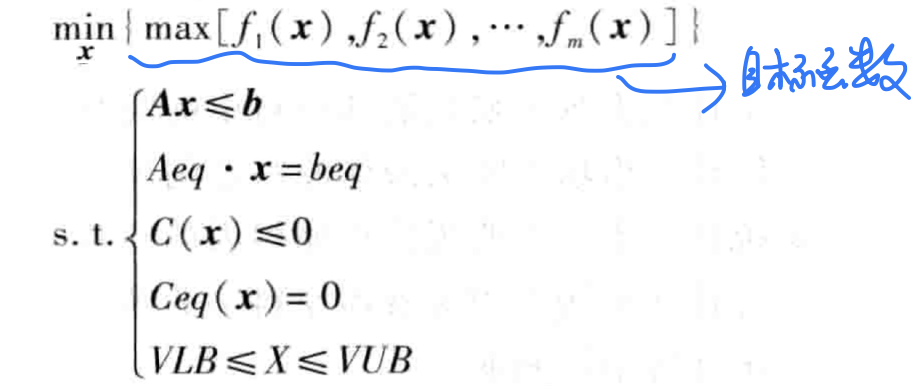
    截屏2023-04-13 15.06.34

[x,fval] = fminimax(@Fun,x0,A,b,[],[],lb,ub)
  • 多目标规划
若一个规划问题中有多个目标, 例如企业在保证利润最大时也要保证生产时产生的污染最少，这种情况下我们可以对多目标函数进行加权组合, 使问题变为单目标规划 , 然后再利用之前学的知识进行求解。

  1. 要先将多个目标函数统一为最大化或最小化问题后才可以进行加权组合

  2. 如果目标函数的量纲不相同, 则需要对其进行标准化后再进行加权, 标准化的方法一般是用目标函数除以某一个常量,该常量是这个目标函数的某个取值 ，具体取何值可根据经验确定（题目给定）

  3. 对多目标函数进行加权求和时, 权重需要由该问题领域的专家给定, 在实际建模比赛中, 若无特殊说明, 我们令权重相同。