多元线性回归分析
绝大多数的数据分析问题,都可以使用回归的思想来解决。
思想:通过研究自变量X和因变量Y的相关关系,尝试去解释Y的形成机制, 达到通过X去预测Y的目的。
因变量Y
连续数值变量:经济学家研究经济增长的决定因素,那么Y可以选取GDP增长率
0-1型变量:P2P公司要研究借款人是否能按时还款,那么Y可以设计成一个二值变量,Y=0时代表可以还款,Y=1时代表不能还款
定序变量:消费者调查得到的数据(1表示非常不喜欢,2表示有点不喜欢,3表示 一般般,4表示有点喜欢,5表示非常喜欢)
计数变量:管理学中RFM模型:F代表一定时间内,客户到访的次数,次数其实就 是一个非负的整数。
生存变量:研究产品寿命、企业寿命甚至是人的寿命
自变量X
X是用来解释Y的相关变量,所以X被称为自变量
X为解释变量,Y为被解释变量
需要完成的使命
- 识别与y有关的重要变量
- 判断相关性方向
- 估计x的不同权重
回归分析的分类
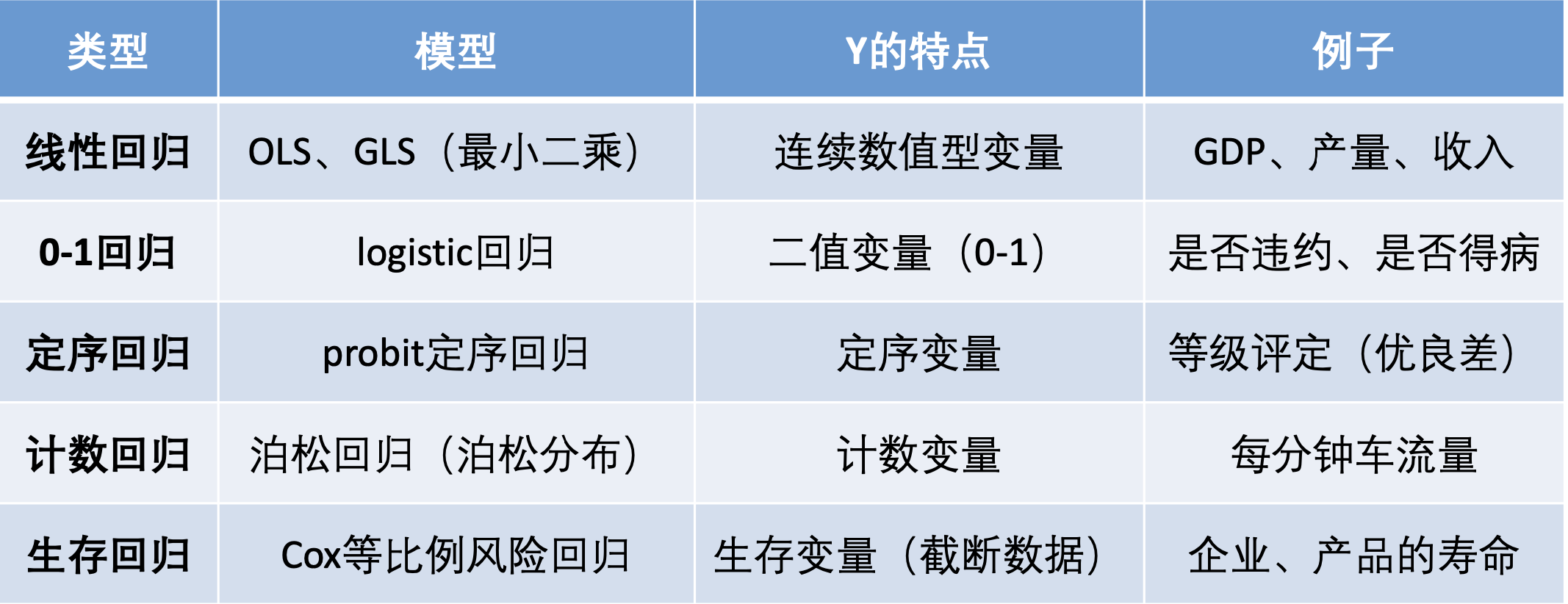
数据的分类
横截面数据:在某一时点收集的不同对象的数据
时间序列数据:对同一对象在不同时间连续观察所取得的数据
面板数据:横截面数据与时间序列数据综合起来的一种数据资源;例如: 2008‐2018年,我国各省份GDP的数据

内生性探讨
\[x是自变量,y是因变量,满足以下关系 \\ y_i = \beta_0 + \beta_1x_i + \mu_i\\ \beta_i 和\beta_1是回归系数,\mu_i是无法观察且满足一定条件的扰动项\\令预测值 \widehat{y_i} = \widehat{\beta_o}+\widehat{\beta_1}x_i \\ 其中\widehat{\beta_0},\widehat{\beta_1} = \mathop{argmin}\limits_{\beta_0,\beta_1}(\sum\limits_{i=1}\limits^n(y_i - \widehat{y_i})^2) = \mathop{argmin}\limits_{\beta_0,\beta_1}(\sum\limits_{i = 1}\limits^n(y_i - \widehat{b_0}-\widehat{\beta_1}x_i)^2)\]
核心解释变量:我们最感兴趣的变量,因此我们特别希望得到对其系数的一致估计(当样本容量无限增大时,收敛于待估计参数的真值 )。
控制变量:我们可能对于这些变量本身并无太大兴趣;而之所以把它们也 放入回归方程,主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素。
在实际应用中,我们只要保证核心解释变量与𝝁不相关即可。
取对数
取对数意味着原被解释变量对解释变量的弹性,即百分比的变化而不是数值的变化;
一元线性回归:𝑦 = 𝑎 + 𝑏𝑥 + 𝜇,x每增加1个单位,y平均变化b个单位;
双对数模型:𝑙𝑛𝑦 = 𝑎 + 𝑏𝑙𝑛𝑥 + 𝜇,x每增加1%,y平均变化b%;
半对数模型:𝑦 = 𝑎 + 𝑏𝑙𝑛𝑥 + 𝜇,x每增加1%,y平均变化b/100个单位;
半对数模型:𝑙𝑛𝑦 = 𝑎 + 𝑏𝑥 + 𝜇,x每增加1个单位,y平均变化(100b)%。
虚拟变量
自变量中对性别、地域等进行研究
将该种变量抽象为虚拟变量,其系数代表虚拟变量的影响