void siftDown(vector<int>& R,int low,int high)
//R[low..high]的自顶向下筛选
{  int i=low;
   int j=2*i+1;			//R[j]是R[i]的左孩子
   int tmp=R[i];			//tmp临时保存根结点
   while (j<=high)			//只对R[low..high]的元素进行筛选
   {  if (j<high && R[j]<R[j+1])
         j++;				//若右孩子较大,把j指向右孩子
      if (tmp<R[j]) 			//tmp的孩子较大
      {  R[i]=R[j];			//将R[j]调整到双亲位置上
         i=j; j=2*i+1;		//修改i和j值,以便继续向下筛选
      }
      else break;			//若孩子较小，则筛选结束
   }
   R[i]=tmp;				//原根结点放入最终位置
}

void siftUp(vector<int>& R,int j)  //自底向上筛选:从叶子结点j向上筛选
{  int i=(j-1)/2; 		      //i指向R[j]的双亲
   while (true)
   {  if (R[j]>R[i])		      //若孩子较大
         swap(R[i],R[j]);	      //交换
      if (i==0) break;	      //到达根结点时结束
      j=i; i=(j-1)/2;		      //继续向上调整
   }
}

void HeapSort(vector<int>& R,int n)	//堆排序
{  for (int i=n/2-1;i>=0;i--)	//从最后一个分支结点开始循环建立初始堆
      siftDown(R,i,n-1);		//对R[i..n-1]进行筛选
   for (int i=n-1;i>0;i--)	//进行n-1趟排序,每一趟后无序区元素个数减1
   {  swap(R[0],R[i]);	//将无序区中尾元素与R[0]交换，扩大有序区
      siftDown(R,0,i-1);		//对无序区R[0..i-1]继续筛选
   }
}

template <typename T>
class Heap			//堆数据结构的实现(默认大根堆)
{  int n;			//堆中元素个数
   vector<T> R;		//用R[0..n-1]存放堆中元素
public:
   Heap():n(0) {}		//构造函数
 
 void siftDown(int low,int high)	//R[low..high]的自顶向下筛选
{  int i=low;
   int j=2*i+1;			//R[j]是R[i]的左孩子
   T tmp=R[i];				//tmp临时保存根结点
   while (j<=high)			//只对R[low..high]的元素进行筛选
   {  if (j<high && R[j]<R[j+1])
         j++;				//若右孩子较大,把j指向右孩子
      if (tmp<R[j])			//tmp的孩子较大
      {  R[i]=R[j];			//将R[j]调整到双亲位置上
         i=j; j=2*i+1;		//修改i和j值,以便继续向下筛选
      }
      else break;			//若孩子较小，则筛选结束
   }
   R[i]=tmp;				//原根结点放入最终位置
}
 
 void siftUp(int j)		//自底向上筛选:从叶子结点j向上筛选
  {  int i=(j-1)/2; 		//i指向R[j]的双亲
     while (true)
     {  if (R[i]<R[j]) 	//若孩子较大，则交换
           swap(R[i],R[j]);
        if (i==0) break;	//到达根结点时结束
        j=i; i=(j-1)/2;	//继续向上调整
     }
  }
  //堆的基本运算算法
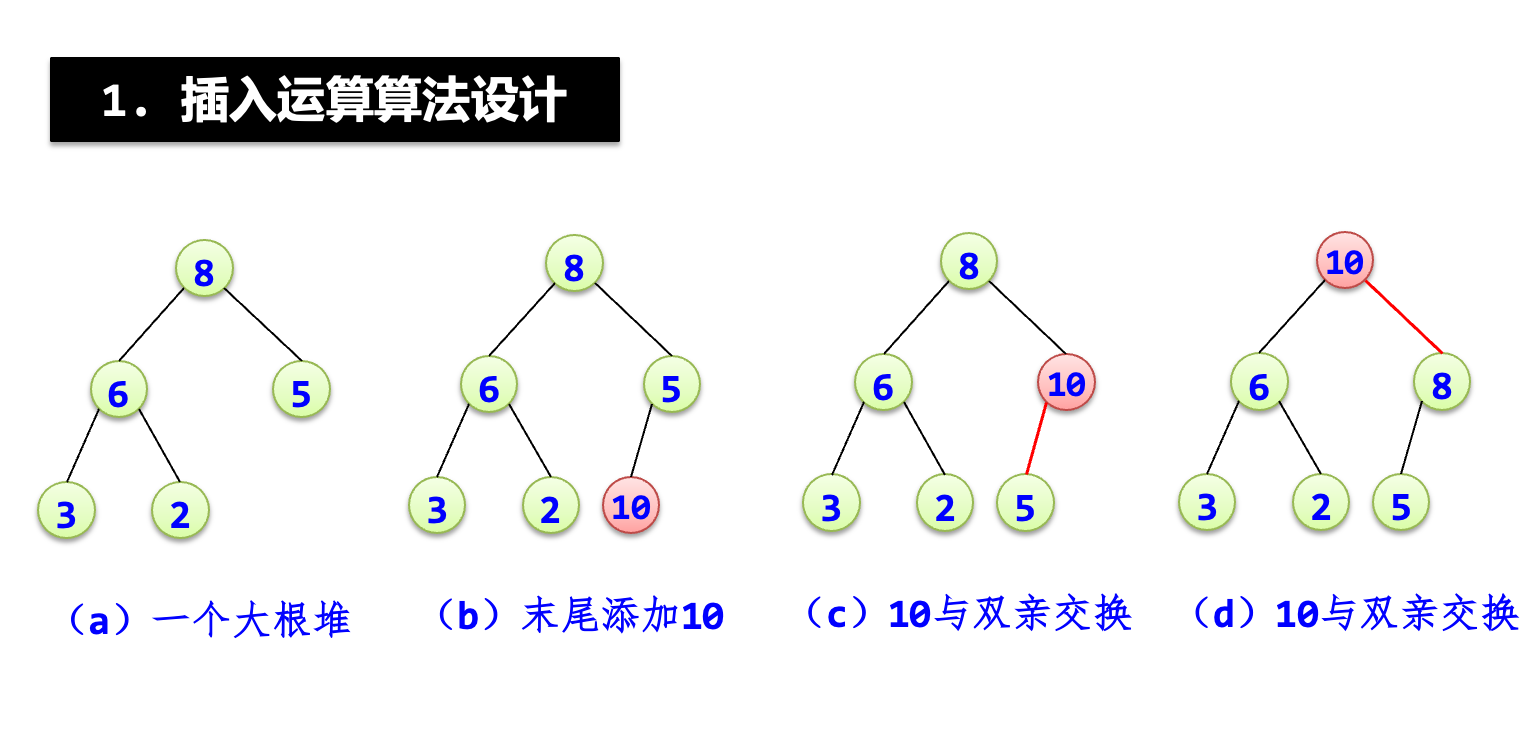
 void push(T e)				//插入元素e
{  n++;					//堆中元素个数增1
   if (R.size()>=n)			//R中有多余空间
      R[n-1]=e;
   else					//R中没有多余空间
      R.push_back(e); 		//将e添加到末尾
   if (n==1) return;			//e作为根结点的情况
   int j=n-1;
   siftUp(j);				//从叶子结点R[j]向上筛选
}

 T pop()				//删除堆顶元素
{  if (n==1)
   {  n=0;
      return R[0];
   }
   T e=R[0];			//取出堆顶元素
   R[0]=R[n-1];		//用尾元素覆盖R[0]
   n--;				//元素个数减少1
   siftDown(0,n-1);		//筛选为一个堆
   return e;
}

 T gettop()	//取堆顶元素
{
   return R[0];
}

 bool empty()	//判断堆是否为空
{
   return n==0;
}
};