二分查找与二分答案

kevin 2024-03-26

算法学习中经常被二分问题困扰（太弱了我），于是记录一下

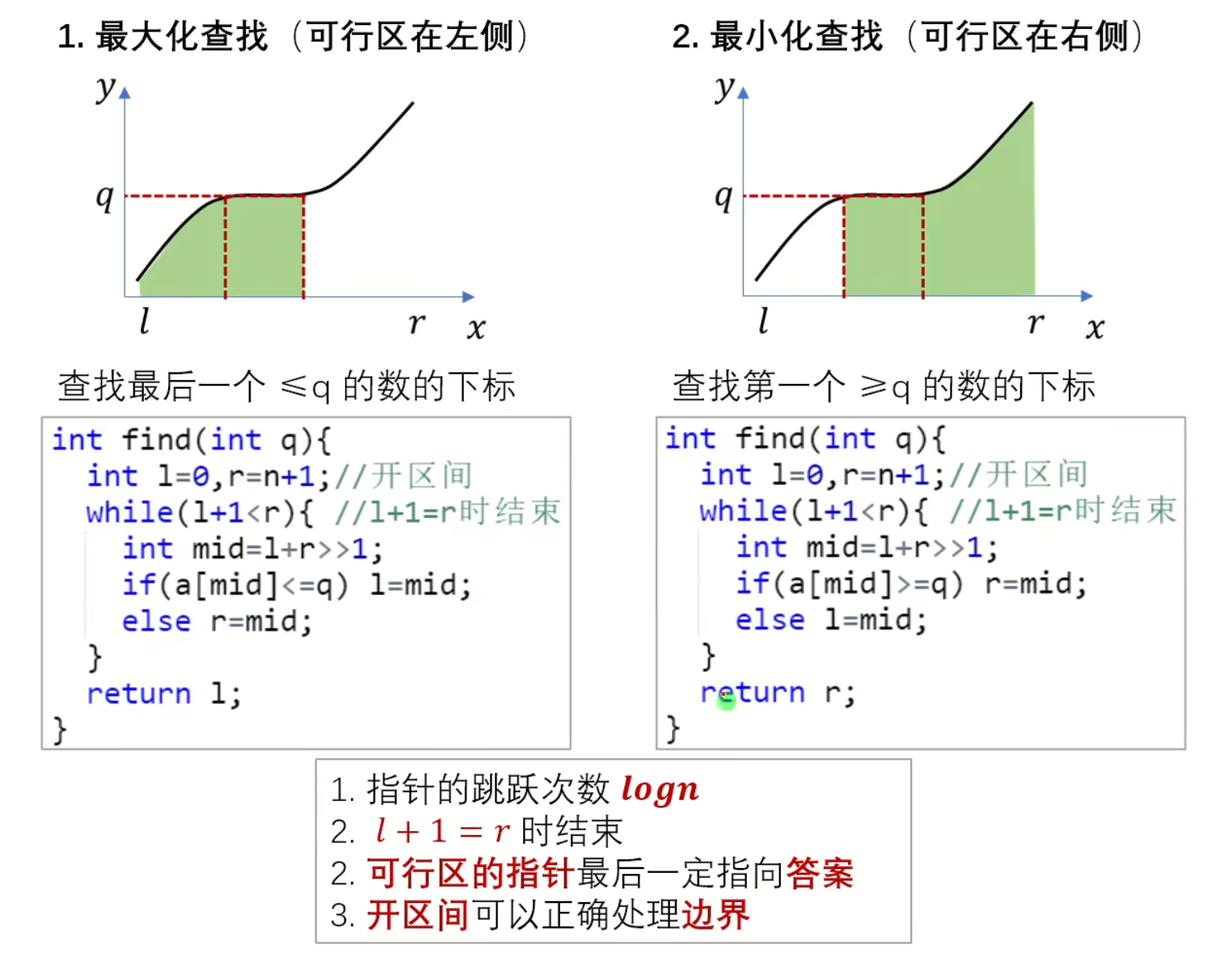
二分查找好用的模板

截屏2024-03-26 20.25.06

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1e5 + 5;

int a[N], q, k, n;

int bsearch_front(int x){
    int l = -1, r = n;
    while( l + 1 < r){
        int mid = (l + r) >> 1;
        if(a[mid] >= x) r = mid;  // if(要找大于等于x的最小的位置) 指向右边则是 r = mid
        else l = mid;
    }
    return r;
}

int bsearch_end(int x){
    int l = -1, r = n;
    while( l + 1 < r){
        int mid = (l + r) >> 1;
        if(a[mid] <= x) l = mid;// if(要找小于等于x的最大的位置) 指向左边则是 l = mid
        else r = mid;
    }
    return l;
}

int main()
{
    cin >> n >> q;

    for (int i = 0; i < n; i ++ )
        cin >> a[i];

    while(q--){
        cin >> k;
        if(bsearch_front(k) == n || bsearch_end(k) == -1 || bsearch_front(k) > bsearch_end(k)) cout <<"-1 -1"<< endl;
        else cout << bsearch_front(k) << " "<< bsearch_end(k) << endl;
    }


}

记忆方法：

当我们寻找大于等于（或大于）x的最小位置时，可行域在右边，指向👉。故在 if 后对r进行赋值，并在最后返回 r 作为查找答案

当我们寻找小于等于（或小于）x的最大位置时，可行域在左边，指向👈。故在 if 后对l进行赋值，并在最后返回 l 作为查找答案

截屏2024-03-27 01.53.14

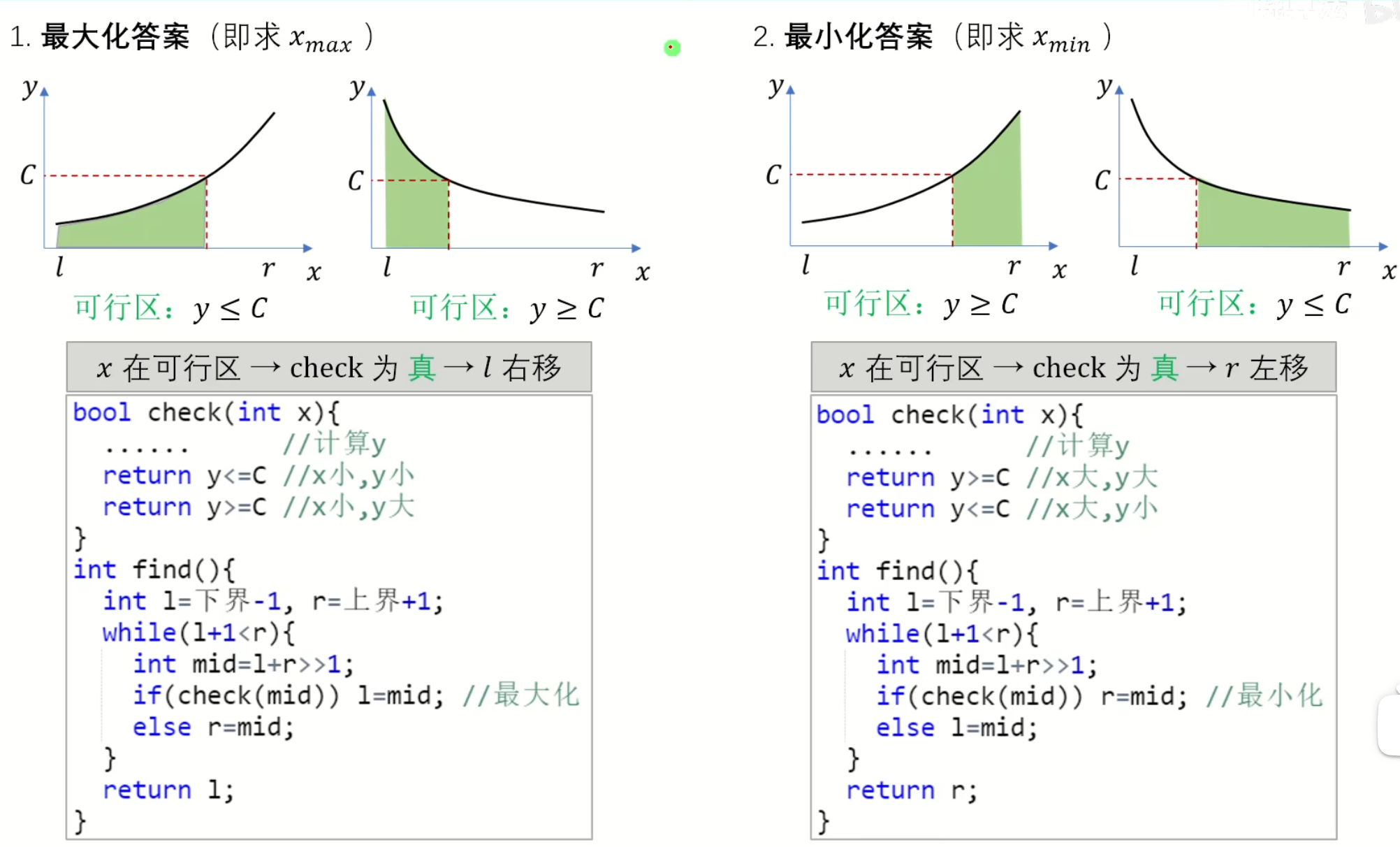
二分答案的模板和例题

截屏2024-03-27 01.44.49

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1e6 + 10;

typedef long long LL;

int d[N], s[N], t[N], r[N];
LL b[N];

int n,m;

bool check(int x){
    for (int i = 1; i <= n; i ++ )
        b[i] = r[i] - r[i-1];
        
        
    for (int i = 1; i <= x; i ++ ){
        b[s[i]] -= d[i];
        b[t[i] + 1] += d[i];
    }
    
    for (int i = 1; i <= n; i ++ ){
        b[i] += b[i-1];
        if(b[i] < 0) return false;
    }
    return true;    
}


int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ){
        cin >> r[i];
        // 容易犯错： b[i] = r[i] - r[i-1];  差分数组
    }
    
    for (int i = 1; i <= m; i ++ ) cin >> d[i] >> s[i] >> t[i];
    
    int l = 0, r = m + 1;
    while(l + 1 < r){
        int mid = l + r >> 1;
        if(check(mid)) l = mid;
        else r = mid;
    }
    
    if(l == m) printf("%d", 0);
    else printf("%d\n%d", -1, l + 1);
    return 0;
}

记忆方法：在二分查找的基础上，把if内判断条件改为check函数

当你设定的可行区在左边👈时（即小于x的情况check函数均返回true），则if后接 l = mid

最后l是满足check的最大解，即最大化可行解，l + 1即不满足

上题中 l == m 当最大值m都满足check时，表示所有订单均成立， l < m则表示 l + 1不满足

截屏2024-03-27 01.46.53